How to write code for 3D FFT in parallel processors
Procedures
1. Decompose the original data into N parts, such as (Nx, Ny, Nz/N), where N is the processor number. Store each of them to distinct GPUs.
2. In the above case, we do 2D FFT in the x-y dimension for Nz/N times, or do two times 1D FFT respectively along X coordinate and along Y coordinate, each with Nz*Ny/N and Nz*Nx/N times.
3. Do a global transpose
4. Do 1D FFT respectively along Z coordinate.
5. Transfer the data back to their original place.
There are two graphs showing the steps described above.
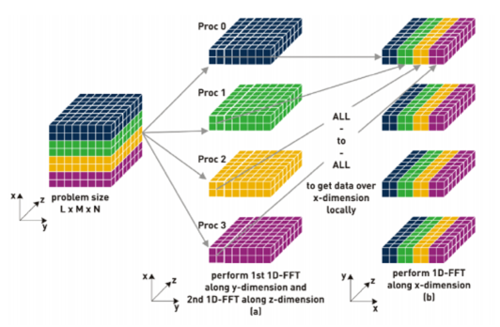
Figure 1: all-to-all comminication (Retrived from: Roland Schulz, "3D FFT with 2D decomposition", 2008)
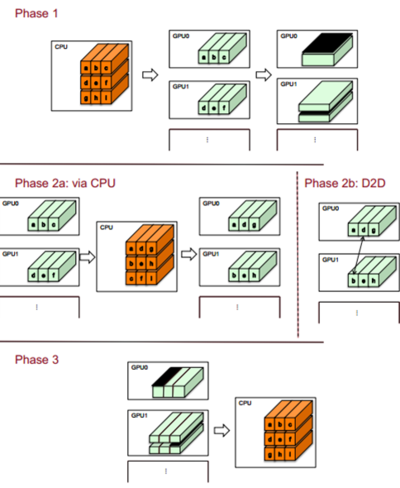
Figure 2: data seperation and transfer (Retrived from: http://cecs.anu.edu.au/files/posters/2012/u4408011.pdf.)
The pseudo code:
// Do 2D FFT in x-y dimension cufftExecZ2Z(plan_2D,p_d,p_d,CUFFT_FORWARD); // Copy data from GPU to CPU; numprocs is the number of processors in parallel cudaMemcpy(p_h,p_d,sizeof(_Complex double)*Nx*Ny*Nz/numprocs,cudaMemcpyDeviceToHost);
// Do a transpose and store data into numprocs arrays with size of Nx*Ny*Nz/(numprocs*numprocs) // Like figure 2 shows transpose(p_h, p_part_h); MPI_Barrier (MPI_COMM_WORLD); // Make sure the transpose operation are all done in every processor // Transfer data in all-to-all communication like figure 1 shows for(int i=0; i<numprocs; i++){ if(i!=rank) MPI_Sendrecv(&p_part_h[i][0], Nx*Ny*Nz/(numprocs*numprocs), MPI_DOUBLE_COMPLEX, i, 0, &p_part_receive_h[i][0], Nx*Ny*Nz/(numprocs*numprocs), MPI_DOUBLE_COMPLEX, i, 0, MPI_COMM_WORLD, &stat); } MPI_Barrier (MPI_COMM_WORLD); // Make sure the transfer operation are all done in every processor
// Coalescing the distinct data in different array into one array coalescing(p_h, p_part_h, p_part_receive_h); // Copy data from CPU to GPU cudaMemcpy(p1ff_d,pf_h,sizeof(_Complex double)*Nx*Ny*Nz/numprocs,cudaMemcpyHostToDevice); // Do 1D FFT along z coordinate cufftExecZ2Z(plan_1D,p_d,p_d,CUFFT_FORWARD); // By this step, 3D FFT computation is finished.
//send back data to its original position in CPU cudaMemcpy(p_h,p_d,sizeof(_Complex double)*Nx*Ny*Nz/numprocs,cudaMemcpyDeviceToHost); transpose(p_h, p_part_h); MPI_Barrier (MPI_COMM_WORLD); for(int i=0; i<numprocs; i++){ if(i!=rank) MPI_Sendrecv(&p_part_h[i][0], Nx*Ny*Nz/(numprocs*numprocs), MPI_DOUBLE_COMPLEX, i, 0, &p_part_receive_h[i][0], Nx*Ny*Nz2/(numprocs*numprocs), MPI_DOUBLE_COMPLEX, i, 0, MPI_COMM_WORLD, &stat); } MPI_Barrier (MPI_COMM_WORLD); coalescing(p_h, p_part_h, p_part_receive_h); // Copy FFT result to GPU cudaMemcpy(p_d,p_h,sizeof(_Complex double)*Nx*Ny*Nz/numprocs,cudaMemcpyHostToDevice);
All the procedures discussed above equal to the following one line code if all of the datas are saved in one GPU cufftExecZ2Z(plan_3D,p_d,p_d,CUFFT_FORWARD);
Issue
For this kind of FFT parallel algorithm executed on multiple GPUs, the all-to-all communication between CPUs occupies about 60% of the total time, and for transpose, coaloscing and cudaMemcpy operation occupies about 30% of the total time. While cufft of 1D and 2D only occupies 5%~10% of the total time. We could see that the overhead of this method is extremely high.